Steady State Power Analysis

Posted on by

I wanted to brush up on the theory before I jump to the implementation. So back to basic circuit analysis.

Instantaneous Power
In a steady state system, the voltage and current as a function of time consists of

v(t)=V_{max}cos(wt + \Theta_v) \qquad(1) i(t)=I_{max}cos(wt + \Theta_i) \qquad(2)

where \Theta_x is is the phase angle of the voltage and current respectively

The instantaneous power is defined as
p(t)=v(t)i(t)=V_{max}I_{max}cos(wt + \Theta_v)cos(wt + \Theta_i)\qquad(3)

Using some trigonometry, (3) reduces to
p(t) = \frac{V_{max}I_{max}}{2}[cos(\Theta_v-\Theta_i) + cos(2wt + \Theta_v + \Theta_i)]\qquad(4)

(4) shows that the instantaneous power has a constant or DC component and a time-variant component and illustrated below.  (v=1, i=1, \Theta_v=\Theta_i=0)

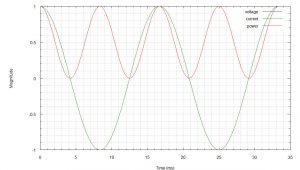
Note the average component “the DC offset” and the frequency of the instantaneous power is two times that of the voltage or current.

We can compute the average power by integrating (4) over one period. We get

P_{avg}=\frac {1}{T}\int^{to+T}_{to}p(t)dt\qquad(5)

If one substitutes (4) into (5), (5) reduces to P=\frac{1}{2}V_{max}I_{max} in a purely resistive circuit and P=\frac{1}{2}V_{max}I_{max}cos(90^\circ) assuming a sinusoidal waveform.

RMS Values
In the power measurement solution for home, one can assume purely resistive loads and sinusoidal voltages and currents. That will come at the price of accuracy. The reality loads such as computers, UPS, etc. introduce inductance and capacitance which create loads that are neither purely resistive nor purely reactive. Furthermore, the current and voltage profiles are not clean sine waves.

Recall that the average power absorbed by a purely resistive load using a sinusoidal source was P_{avg}=\frac{1}{2}V_{max}I_{max}. Note that if the source was a DC, then P_{avg}=I^2R What if the source is not a sinusoidal wave? Is there an equivalent constant current that can be computed that delivers the same average power to a purely resistive load (R)? .e.g. P_{avg} = I^2_{equiv}R =\frac {1}{T}\int^{to+T}_{to}i^2(t)Rdt solving for I_{equiv} we get

I_{equiv}=I_{rms}=\sqrt{\frac {1}{T}\int^{to+T}_{to}i^2(t)dt} \qquad(6)

Plug in in a sinusoidal current like i(t)=I_{max}cost(wt + \Theta)\quad T=\frac{2\pi}{w} into (6) we get the infamous I_{rms}=\frac{I_{max}}{\sqrt{2}}

Given this view of the RMS current, one can write the average power as

P_{avg} = V_{rms}I_{rms}cos(\Theta_v-\Theta_i) \qquad(7)) In the North-American 120 volt system, the 120 is the RMS voltage and V_{max} = 120\sqrt{2}\approx 170V

For non-sinusoidal functions, more complex integration needs to occur. Fortunately, in the implementation, there are some assumptions we can make to approximate the integration that makes the math much simpler. Nevertheless, an understanding of the math is needed to bend the rules.

Power Factor
One last component needs to be addressed and that is the power factor. Equation (7) contains two components. The product of V_{rms}I_{rms} is known as the Apparent Power (S) and the cos(\Theta_v-\Theta_i) as the Power Factor.

In an purely resistive circuit, P_{avg}=P_{apparent} since cos(\Theta_v-\Theta_i) = 1

Moving Forward

The reference implementation shall compute the average power, Irms and Vrms. Using (7), one can compute the power factor. e.g. \frac{P_{avg}}{V_{rms}I_{rms}} = PF

The power factor angle = arccos{\frac{P_{avg}}{V_{rms}I_{rms}}}   The reactive power can be computed by the relation S^2 = P^2_{avg} + Q^2 where Q is the reactive power in vars. Solve for Q and we can now compute all power related components.

Now you may ask why the Power Factor Angle? We don’t even reference it? Well, you could use to compute the reactive power. What it does give me is sense of the types of loads I have in the house. A value closer to 0, implies I am operating in a resistive load. If you look at the power factor angle of a variable speed drill, at low speeds the angle would be far from zero. At full RPM the angle would approach zero. Why this is the case is because how variable speed drills work. That is a separate discussion.

Next I want to model the math using a tool to help me make some assumptions for my reference implementation.

Home Power Monitoring

Posted on by

Back in the day I used to read Byte magazine and faithfully read Steve Ciarcia’s articles. I went down a career path that did not include much in terms of pure engineering and left it as a distant memory. I recently decided it was high time to renew my hobby in tinkering with electronics and software. Fortunately, Steve is still around at Circuit Cellar with a group of dedicated writers willing to share their experiences with their readers.  I will never make a living in designing electronics and embedded systems nor do I want to. As a hobby, good enough is good enough for me.

My first project will be home power monitoring. The end-goal is to install solar modules on the roof and I would like to trend environmental information both inside and outside of the home so I can baseline my power consumption profile. True one can purchase technology to measure power but where would the fun be in that? 

Functional Requirements

Real-time Information
RMS current, RMS voltage, power factor, power factor angle, apparent power, real power, reactive power

Temperature – this will be a separate project to measure external and internal temperatures throughout the home. I felt that adding a temperature measurement  is trivial and will not add too much complexity to the project.

Historical Data
Average, Max, Min, Median of real-time data derived from data historian

Communications
Over mesh network at home. I want to include other devices around the house from which all data aquistion will be collected by a data concentrator. Not sure what the data concentrator will be at this point.

Human Machine Interface
Simple LCD to display real-time information at the point of measurement

Web and iphone viewing of near-real-time and historical data.

Technology
Do as much work using open source software.

Utilize an affordable and easy to use embedded system so that my kids might take interest in learning electronics and interfacing

Well off to the races I go.